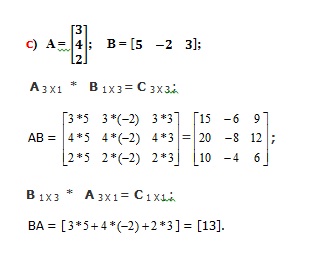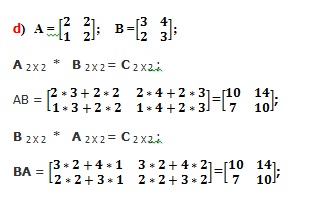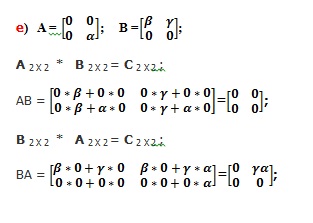1. Să se calculeze determinantul prin regula lui Sarrus:

Δ₃ = a₁₁ a₂₂ a₃₃ + a₂₁ a₃₂ a₁₃ + a₃₁ a₁₂ a₂₃  - a₁₃ a₂₂ a₃₁- a₂₃ a₃₂ a₁₁- a₃₃ a₁₂ a₂₁;

a)

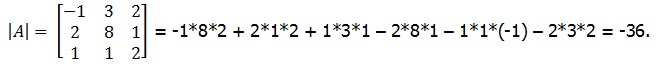
b)

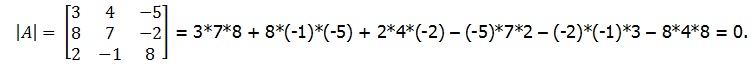
c)

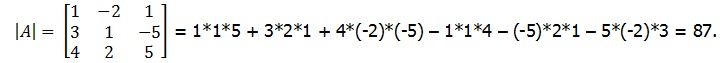
Codul C#:

using System;

namespace detSarrusMetod
{
    class Program
    {
        static void Main(string[] args)
        {

            Console.WriteLine("\n Calculare determinant prin metoda lui Sarrus (triunghiului):");
            Console.WriteLine("\n Introduceti elementele matricei: \n");

            int[,] matrixA = new int[3, 3];

            //----------introducere elemente matrice--------------------------------------------------------

            for (int i = 0; i < 3; i++)
            {
                for (int j = 0; j < 3; j++)
                {
                    matrixA[i, j] = int.Parse(Console.ReadLine());

                }
            }
            //----------afisare matrice--------------------------------------------------------
            Console.WriteLine("\n Matricea este: \n");
            for (int i = 0; i < matrixA.GetLength(0); i++)                //matrixA.GetLength(0) extrage numarul de rimduri
            {
                for (int j = 0; j < matrixA.GetLength(1); j++)            //matrixA.GetLength(1) extrage numarul de coloane
                {
                    Console.Write(string.Format(" {0} ", matrixA[i, j]));
                }
                Console.Write(Environment.NewLine + Environment.NewLine);
            }
            //----------calculare determinant---------------------------------------------------
            int detSarrus = (matrixA[0, 0] * matrixA[1, 1] * matrixA[2, 2]) +
                                 (matrixA[0, 1] * matrixA[1, 2] * matrixA[2, 0]) +
                                 (matrixA[0, 2] * matrixA[1, 0] * matrixA[2, 1]) -
                                 (matrixA[0, 2] * matrixA[1, 1] * matrixA[2, 0]) -
                                 (matrixA[0, 0] * matrixA[1, 2] * matrixA[2, 1]) -
                                 (matrixA[0, 1] * matrixA[1, 0] * matrixA[2, 2]);

            //----------afisare formula---------------------------------------------------

            Console.WriteLine("Formula de calcul: \n" + "(" + matrixA[0, 0] + "*" + matrixA[1, 1] + "*" + matrixA[2, 2] + ")" + " + "
                                                      + "(" + matrixA[0, 1] + "*" + matrixA[1, 2] + "*" + matrixA[2, 0] + ")" + " + "
                                                      + "(" + matrixA[0, 2] + "*" + matrixA[1, 0] + "*" + matrixA[2, 1] + ")" + " - "
                                                      + "\n(" + matrixA[0, 2] + "*" + matrixA[1, 1] + "*" + matrixA[2, 0] + ")" + " - "
                                                      + "(" + matrixA[0, 0] + "*" + matrixA[1, 2] + "*" + matrixA[2, 1] + ")" + " - "
                                                      + "(" + matrixA[0, 1] + "*" + matrixA[1, 0] + "*" + matrixA[2, 2] + ")");

            //--------------afisare determinant-------------------------------------------------
            Console.WriteLine("Determinantul matricei A este: " + detSarrus);

            //--------------asteapta tastare----------------------------------------------------
            Console.ReadKey(true);
        }
    }
}

2. Să se calculeze determinantul prin reducerea ordinului:

a)

            (1) => Rind_3 = Rind_3 - Rind_2;

            (2) => Coloana_2 = Coloana_2 - Coloana_3 * 2;

                 => Coloana_1 = Coloana_1 - Coloana_3 * 2;

b)

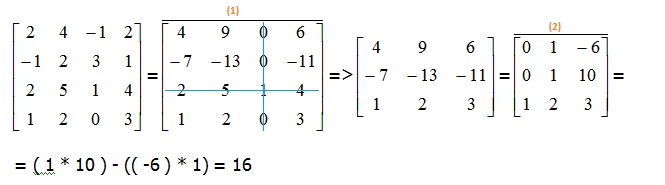
            (1) => Rind_1 = Rind_1 + Rind_3;

                 => Rind_2 = Rind_2 - Rind_3 * 3;

            (2) => Rind_1 = Rind_1 - Rind_3 * 4;

                 => Rind_2 = Rind_2 + Rind_3 * 7;

3. Să se calculeze determinantul prin aducere la forma triunghiulara:

a)

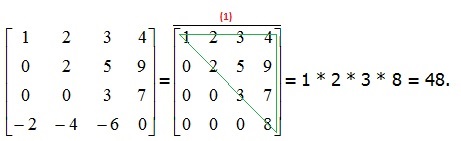
           (1) => Rind_4 = Rind_4 + Rind_1 * 2;

b)

            (1) => Rind_2 = Rind_2 - Rind_1;

                 => Rind_3 = Rind_3 - Rind_1;

                 => Rind_4 = Rind_4 - Rind_1;

            (2) => Rind_4 = Rind_4 - Rind_2 * 4;

                 => Rind_3 = Rind_3 - Rind_2 * 5;

            (3) => Rind_4 = Rind_4 - Rind_3 * 5/6;

4. Să se calculeze determinantul :

a)

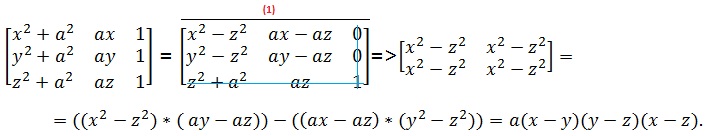
            (1) => Rind_1 = Rind_1 - Rind_3;

                 => Rind_2 = Rind_2 - Rind_3;

b)

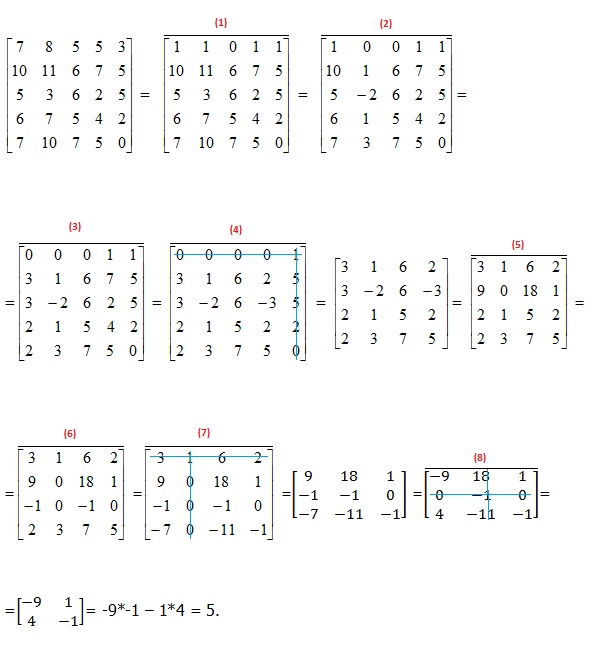
            (1) => Rind_1 = Rind_1 - Rind_4;

            (2) => Col_2 = Col_2 - Col_1;

            (3) => Col_1 = Col_1 - Col_4;

            (4) => Col_4 = Col_4 - Col_5;

            (5) => Rind_2 = Rind_2 + Rind_1 * 2;

            (6) => Rind_3 = Rind_3 - Rind_1;

            (7) => Rind_4 = Rind_4 - Rind_1 * 3;

            (8) => Col_1 = Col_1 - Col_2;

c)

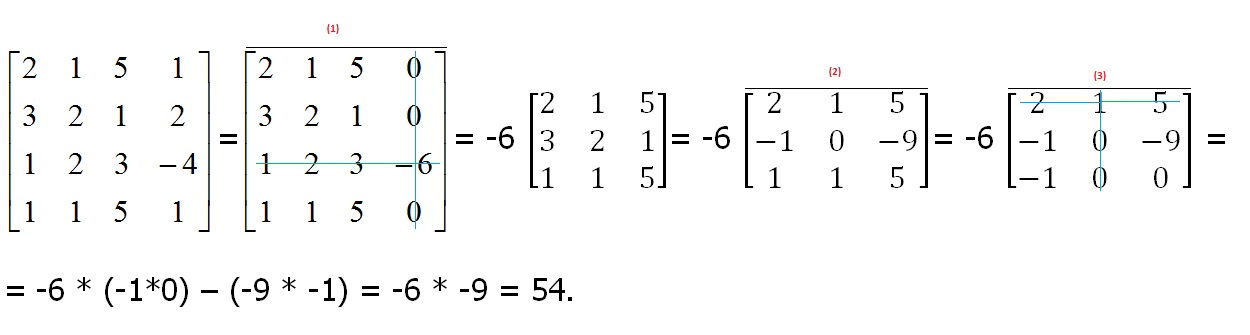
            (1) => Col_4 = Col_4 - Col_2;

            (2) => Rind_2 = Rind_2 - Rind_1 * 2;

            (3) =>Rind_3 = Rind_3 - Rind_1;

d)

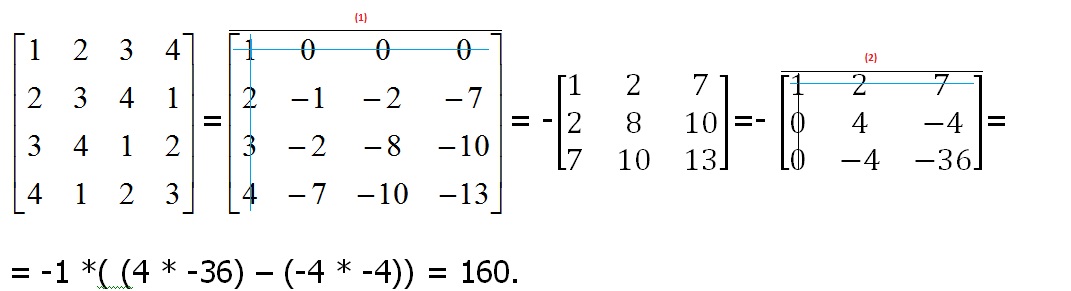
            (1) => Col_2 = Col_2 - Col_1 * 2;

                 => Col_3 = Col_3 - Col_1 * 3;

                 => Col_4 = Col_4 - Col_1 * 4;

            (2) => Rind_2 = Rind_2 - Rind_1 * 2;

                 =>Rind_3 = Rind_3 - Rind_1 * 7;

1. Fie matricele A si B. De calculat: A + B, 2A, A – 3B, daca:

2. Fie matricele A si B. De calculat: AB, BA, daca: